2 kroky řešení
Polynomy - ![]() speciální metody
speciální metody
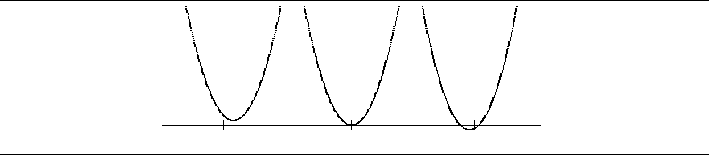
Dvojnásobné kořeny - hledání řešení v reálném oboru v okolí
dvojnásobného kořenu =
nekorektní úloha
libovolně malá změna koeficientů může
![]() .
.
Pozn. V komplexním oboru je úloha vždy korektní.
Pozn. Hledání dvojnásobného kořene se provádí pomocí hledání extrému.
Ohraničení kořene -
Pokud pro ![]() platí, že
platí, že
![]() je
v intervalu
je
v intervalu ![]() alespoň jeden kořen.
alespoň jeden kořen.
Algoritmus ohraničení spočívá v rozšiřování, příp. zkracování
původně navrženého intervalu.
Hledání ohraničeného kořene -
Obvykle metody, které nepoužívají derivace.
Užití derivace
![]() derivace analytický vzorec
derivace analytický vzorec ![]() rychlý
numerický výpočet.
rychlý
numerický výpočet.