Newton-Raphsonova (tečnová) metoda

Využívá první derivaci zadané funkce, proto je vhodná zejména pokud lze hodnoty derivací rychle počítat. Zadanou funkci $f(x)$ rozvineme do Taylorova rozvoje v okolí bodu $x_i$. Je-li $x = x_i + \delta$, pak platí

$$f(x) = f(x_i + \delta) = f(x_i) + \delta f'(x_i) + \frac{\delta^2}{2} f''(x_i) + \dots$$

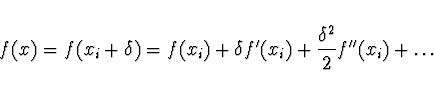
Nahradíme Taylorovu řadu tečnou přímkou, $\delta$ přibližně určíme z podmínky

$$\delta = - \frac{f(x_i)}{f'(x_i)}\ \Rightarrow \ x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)}$$

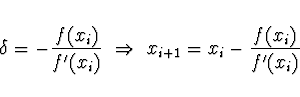
Pro nepřesnost $(i+1)$-ní aproximace kořene platí

$$\epsilon_{i+1} = \epsilon_i + \delta = \epsilon_i + \frac{f(x_i)}{f'(x_i)} \simeq - \epsilon_i^2\ \frac{f''(x_i)}{2\, f'(x_i)}$$

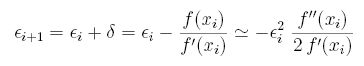
Newton-Raphsonova metoda je tedy kvadratická metoda $\rightarrow$ rychlá blízko u kořene. Konvergence není zaručená, nutná kontrola ohraničení kořene a kombinace s metodou půlení intervalů.