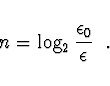Po
Platí
Nechť je kořen ohraničen
![]() , tak že
, tak že
![]() . Označme
. Označme
![]() .
Jeden krajní bod ponecháme a druhý posuneme do
.
Jeden krajní bod ponecháme a druhý posuneme do ![]() tak, aby opět platilo
tak, aby opět platilo
![]() .
.
Po ![]() -tém kroku kořen omezený body
-tém kroku kořen omezený body ![]() a
a ![]() a
nepřesnost určení kořene je
a
nepřesnost určení kořene je
![]() .
.
Platí
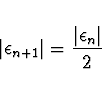
Pozn. Obecně lze zapsat
![]() , kde
, kde ![]() .
.
Půlení intervalů je lineární metoda ![]() a
a
![]() .
.
Počet kroků pro výpočet kořene s přesností ![]() je
při počáteční chybě
je
při počáteční chybě ![]() roven
roven