Laser beam profile diagnostics
Introduction
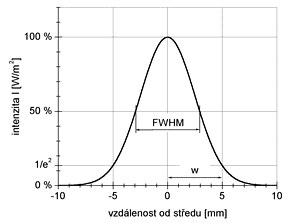 Fig. 7.1: The sample of Gaussian profile.
Fig. 7.1: The sample of Gaussian profile.where I is the intensity, ρ is a radial coordinate, P is a total power, w is beam semidiameter (called radius), and z is a axial coodinate. This is a convention in laser physics. In most other fields, the parameter describing FWHM is σ – a standard deviation. Be very carefull to recognize these two conventions, because is not a direct substition of w. The correct relation is w = 2σ. To describe any laser output (a combination of several modes) by the same formalism as a fundamental one the parameter M2 - a beam quality factor - is defined. It is 1 for ideal single mode lasers and up to several 100 for multimode lasers, see ref.
The image take from CCD is called saturated when contain several points with maximum intensity value (defined by A/D converter) and observer cannot decide the intensity ratio between them. Avoid this situation.
Goal
Using CCD camera record beam profiles of fundamental transverse mode of expanded HeNe laser. Estimate beam radius in two perpendicular axis.
Instructions
- Use HeNe laser with beam expander. Keep laser output beam propagate several decimeters. Insert screen into laser beam.
- Take beam profile exposures by CCD camera. Be carefull to setup right camera shading and/or laser beam attenuation to avoid image saturation. Record the distance of screen from laser head.
- Take a reference exposure with scaled paper to have information about image scale.
- Process beam profiles in any suitable program, choise apposite cartesian coordinate system, fit profiles by Gaussian function, record beam radii and using scaling images convert radii to absolute units.
Requested results
- 3D graph (x,y,I) of one selected transversal beam profile. In description its distance from laser head.
- Two intenzity profile graphs (x,I) and (y,I) with independent Gaussian fits.
- Two beam radia [mm]. (i.e. one of results of above mentioned fits)
References
- Melles Griot - Non-Gaussian Laser Beams theory
- http://beammeasurement.mellesgriot.com/tut_Gaussian_beam_prop.asp#nglb
- MEOS EXP 08 laser kit
- http://www.meos.com/Laser%20fundaments/Diode%20pumped.htm
Czech Technical University in Prague - Faculty of Nuclear Sciences and Physical Engineering
Brehova 7, 115 19 Prague 1, Czech Republic