Studentovo ![]() -rozdělení o
-rozdělení o ![]() stupních volnosti
má hustotu pravděpodobnosti definovanou vztahem
stupních volnosti
má hustotu pravděpodobnosti definovanou vztahem
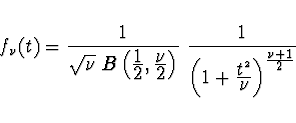
Rozdělení odchylky průměru od střední hodnoty
Nech»
![]() je prostý výběr z normálního
rozdělení
je prostý výběr z normálního
rozdělení
![]() , nech»
, nech» ![]() je výběrový průměr a
nech»
je výběrový průměr a
nech» ![]() je výběrová směrodatná odchylka. Pak veličina
je výběrová směrodatná odchylka. Pak veličina
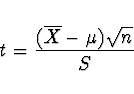
Pozn. Veličina ![]() je vlastně relativní odchylka výběrového
průměru - odchylka průměru od střední hodnoty dělená odhadovanou
směrodatnou odchylkou
je vlastně relativní odchylka výběrového
průměru - odchylka průměru od střední hodnoty dělená odhadovanou
směrodatnou odchylkou ![]() výběrového průměru.
výběrového průměru.
Odvození Veličina
![]() má rozdělení
má rozdělení ![]() a veličina
a veličina
![]() má rozdělení
má rozdělení
![]() . Tyto veličiny jsou navzájem nezávislé a lze tedy sestrojit
hustotu pravděpodobnosti
. Tyto veličiny jsou navzájem nezávislé a lze tedy sestrojit
hustotu pravděpodobnosti ![]() . Veličina
. Veličina
![]() ,
provedeme transformací proměnných, Jacobián transformace
,
provedeme transformací proměnných, Jacobián transformace
![]() .
Dvourozměrnou rozdělovací funkci
.
Dvourozměrnou rozdělovací funkci ![]() integrujeme přes
proměnnou U.
integrujeme přes
proměnnou U.