Rozdělení $\chi^2 (n)$ o n stupních volnosti

Nechť $\{ X_{1},X_{2},\dots,X_{n} \}$ je prostý výběr z normálního rozdělení $N(0,1)$. Pak veličina $W = \sum_{i=1}^n X_i^2$ má rozdělení $\chi^2 (n)$ o n stupních volnosti s hustotou pravděpodobnosti

$$f(w) = \frac{1}{\Gamma \left( n/2 \right) 2^{(n/2)}}\ {\rm e}... ...ptstyle 2}}} w^{\frac{{\scriptstyle n}}{{\scriptstyle 2}} - 1}$$

kde funkce $\Gamma (\alpha ) = \int_0^\infty x^{\alpha - 1} {\rm e}^x {\rm d}x$ (pro celá $k$ je $\Gamma (k+1) = k!$).

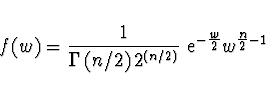
Střední hodnota $EW=n$, rozptyl $DW = 2n$ a charakteristická funkce $\Psi_W (t) = ( 1 - 2it)^{-n/2}$.

Rozdělení výběrového rozptylu $S^2$ pro výběr z normálního rozdělení

Pro prostý náhodný výběr z rozdělení $N(\mu,\sigma^2)$ má veličina $W = (n-1) S^2 / \sigma^2$ rozdělení $\chi^2 (n-1)$ o $n - 1$ stupních volnosti.

Pozn. Při výpočtu $S^2$ z výběru o rozsahu $n$ je místo střední hodnoty $EX$ použit výběrový průměr $\overline{X}$, a tedy diference $X_i - \overline{X}$ nejsou navzájem nezávislé. Vektorový prostor definovaný vektory $X_i - \overline{X}$ má dimenzi $n - 1$ = počet dat $-$ počet použitých parametrů z dat odvozených. Rozdělení $S^2$ má tedy $(n - 1)$ stupňů volnosti.