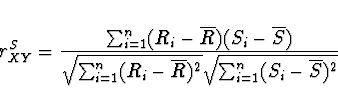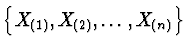 vznikne uspořádáním prvků výběru
vznikne uspořádáním prvků výběru
Uspořádaný výběr
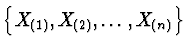 vznikne uspořádáním prvků výběru
vznikne uspořádáním prvků výběru
![]() vzestupně podle velikosti.
vzestupně podle velikosti.
Výběrový p-kvantil ![]() je pro
je pro ![]() definován
předpisem
definován
předpisem
![\begin{displaymath}\tilde{x}_p = \left\{ \begin{array}{ll}X_{([np]+1)} & np \not...
...(np)} + X_{(np+1)} \right) & np \in \cal{N} \end{array}\right. \end{displaymath}](img50.gif)
Korelace pořadí - Spearmanův korelační koeficient
Nechť při prostém výběru o rozsahu ![]() jsou
sledovány dva znaky
jsou
sledovány dva znaky ![]() a
a ![]() . Dostaneme dva soubory hodnot
. Dostaneme dva soubory hodnot
![]() a
a ![]() , kde
, kde ![]() je index prvku výběrového souboru.
Označme
je index prvku výběrového souboru.
Označme ![]() (resp.
(resp. ![]() ) pořadí i-tého prvku podle velikosti
v souboru hodnot
) pořadí i-tého prvku podle velikosti
v souboru hodnot ![]() (resp.
(resp. ![]() ). Pro názornost označíme průměrnou
hodnotu pořadí
). Pro názornost označíme průměrnou
hodnotu pořadí
![]() . Pak
Spearmanův korelační koeficient je dán
. Pak
Spearmanův korelační koeficient je dán