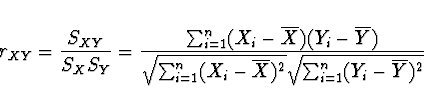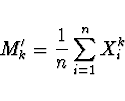
Výběrový obecný moment - K-tý výběrový obecný (počáteční) moment
je dán vztahem
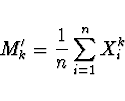
Výběrový průměr je
![]() .
Platí-li pro prostý náhodný výběr
.
Platí-li pro prostý náhodný výběr
![]() a
a
![]() ,
pak střední hodnota výběrového průměru
,
pak střední hodnota výběrového průměru
![]() a rozptyl
a rozptyl
![]() . Výběrový průměr je tedy vhodný
pro odhad střední hodnoty rozdělení.
. Výběrový průměr je tedy vhodný
pro odhad střední hodnoty rozdělení.
Výběrový centrální moment - K-tý výběrový centrální moment
je dán vztahem
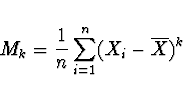
Výběrový rozptyl - je dán vztahem
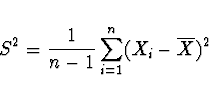
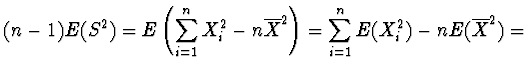 |
|||
![$\displaystyle \sum_{i=1}^n \left[
E^2 (X_i) + D(X_i) \right] - n \left[ E^2 (\o...
...D(\overline{X})
\right] = n (\mu^2 + \sigma^2) - n (\mu^2 + \frac{\sigma^2}{n})$](img23.gif) |
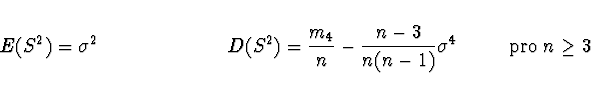
Pozn. - Protože ![]() je vypočten z hodnot
je vypočten z hodnot ![]() výběrového souboru, je z
výběrového souboru, je z ![]() hodnot odchylek
hodnot odchylek
![]() jen
jen
![]() hodnot lineárně nezávislých, proto musíme dělit výrazem
hodnot lineárně nezávislých, proto musíme dělit výrazem
![]() a rozdělení náhodné veličiny
a rozdělení náhodné veličiny ![]() má
má ![]() stupňů volnosti.
stupňů volnosti.
Výběrová směrodatné odchylka je
![]() .
.
Střední hodnota
![]() je obvykle menší než
je obvykle menší než ![]() , neb
, neb
![]() . Tedy
. Tedy ![]() pouze tehdy, pokud
pouze tehdy, pokud ![]() .
.
Výběrová kovariance Nechť při prostém výběru o rozsahu ![]() jsou
sledovány dva znaky
jsou
sledovány dva znaky ![]() a
a ![]() . Dostaneme dva soubory hodnot
. Dostaneme dva soubory hodnot
![]() a
a
![]() .
Výběrová kovariance
.
Výběrová kovariance ![]() je dáma vztahem
je dáma vztahem
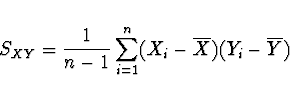
Výběrový lineární korelační koeficient