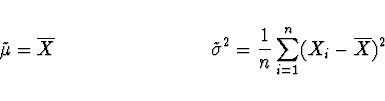Nechť
Často se odhady konstruují ad hoc.
Ukážeme si však 2 obecné metody konstrukce odhadů.
A) Momentová metoda
Nechť ![]() je prostý náhodný výběr z rozdělení
je prostý náhodný výběr z rozdělení
![]() ,
kde
,
kde
![]() je vektor neznámých parametrů rozdělení. Nechť
je vektor neznámých parametrů rozdělení. Nechť
![]() existuje konečný obecný moment
existuje konečný obecný moment
![]() pro
pro
![]() .
Všechny momenty lze vyjádřit jako funkce parametrů
.
Všechny momenty lze vyjádřit jako funkce parametrů ![]() následovně
následovně
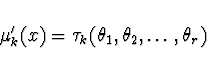
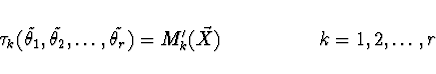
Věta Odhady, provedené momentovou metodou, jsou konzistentní.
Příklad Nechť rozdělení má distribuční funkci
![\begin{displaymath}F(x;\vec{\alpha}) = \left\{ \begin{array}{ll}0 & x \le \alpha...
...[-\alpha_2 (x - \alpha_1) ] & x > \alpha_1 \end{array} \right. \end{displaymath}](img157.gif)
Řešení
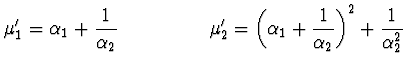 |
|||
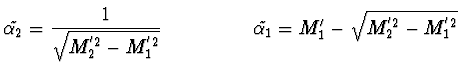 |
B) Metoda maximální věrohodnosti
Pro prostý výběr ![]() ze spojitého rozdělení vypočteme hustotu
pravděpodobnosti
ze spojitého rozdělení vypočteme hustotu
pravděpodobnosti
![]() výběru
výběru ![]() pro
danou hodnotu
pro
danou hodnotu ![]() (pro výběr z diskrétního rozdělení vypočteme
pravděpodobnostní funkci
(pro výběr z diskrétního rozdělení vypočteme
pravděpodobnostní funkci
![]() ). Pak jako odhad
parametrů vybereme taková
). Pak jako odhad
parametrů vybereme taková ![]() , při
nichž nastává
, při
nichž nastává
![]() (respektive
(respektive
![]() ).
).
Vysvětlení
Parametry rozdělení vybereme z množiny možných parametrů tak,
aby při nich bylo dané pozorovaní nejpravděpodobnější.
Pozn. Nemusíme hledat přímo extrém ![]() či
či ![]() , ale lze hledat extrém
jejich monotonní funkce. Pro prostý náhodný výběr jsou
, ale lze hledat extrém
jejich monotonní funkce. Pro prostý náhodný výběr jsou ![]() vzájemně
nezávislé a tedy
vzájemně
nezávislé a tedy

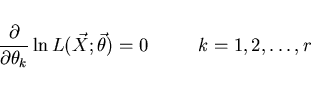
Příklad Pomocí metody maximální věrohodnosti z výběru ![]() odhadněte parametry
odhadněte parametry
![]() normálního rozdělení
normálního rozdělení
![]() .
.
Řešení
![$\displaystyle \prod_{i=1}^n \frac{1}{\sqrt{2\pi} \sigma}
\exp \left[ \frac{(X_i...
...a} \right)^n \exp \left[ - \sum_{i=1}^n
\frac{(X_i -\mu)^2}{2 \sigma^2} \right]$](img177.gif) |
|||
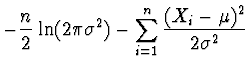 |
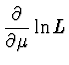 |
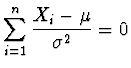 |
||
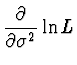 |
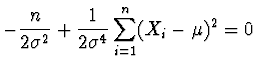 |