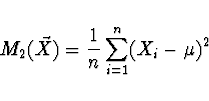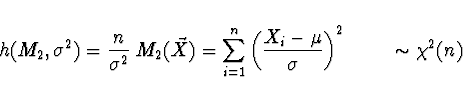Bodový odhad parametru neumožňuje přímo zjistit, jak blízko leží skutečný
parametr k odhadu. Často je potřebné zjistit oblast, kde se skutečný
parametr s velkou pravděpodobností nachází. K tomu slouží intervalové
odhady.
Definice Nechť ![]() ,
, ![]() jsou dvě
výběrové statistiky takové, že
jsou dvě
výběrové statistiky takové, že
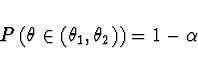
Postup Obecně neexistuje způsob, jak sestrojit
podmíněné rozdělení pravděpodobnosti (distribuční funkci)
![]() při daném výběru.
Zvolíme vhodný bodový odhad
při daném výběru.
Zvolíme vhodný bodový odhad ![]() parametru
parametru ![]() . Sestrojíme
podmíněné rozdělení pravděpodobnosti
. Sestrojíme
podmíněné rozdělení pravděpodobnosti
![]() bodového odhadu
bodového odhadu ![]() .
Pro funkci
.
Pro funkci ![]() monotonní v
monotonní v ![]() pro konstantní
pro konstantní ![]() , která splňuje podmínku
, která splňuje podmínku
![]() nezávisí na
nezávisí na ![]() , definujeme
, definujeme
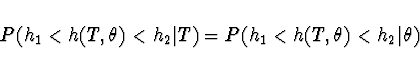
Pozn. Protože lze obecně sestrojit více funkcí ![]() , není
určení intervalového odhadu jednoznačné. Intervalové odhady souvisí
úzce s testováním hypotéz, proto se k nim ještě vrátíme v následující
kapitole.
, není
určení intervalového odhadu jednoznačné. Intervalové odhady souvisí
úzce s testováním hypotéz, proto se k nim ještě vrátíme v následující
kapitole.
Pozn. Nejčastěji hledáme symetrické intervaly spolehlivosti
![]() .
Užívají se ale i jednostranné intervalové odhady, např.
.
Užívají se ale i jednostranné intervalové odhady, např.
![]() s parametrem spolehlivosti
s parametrem spolehlivosti ![]() ,
tedy interval
,
tedy interval
![]() .
.
Příklad Nechť ![]() je výběr z normálního rozdělení
je výběr z normálního rozdělení
![]() se známou střední hodnotou
se známou střední hodnotou ![]() . Nalezněte
konfidenční interval
. Nalezněte
konfidenční interval ![]() s parametrem spolehlivosti
s parametrem spolehlivosti ![]() .
.
Řešení