Předpokládáme, že známe typ rozdělení náhodné veličiny, ale neznáme jeho
některé parametry. Např. víme, že rozdělení je normální
![]() ,
ale neznáme
,
ale neznáme ![]() a
a ![]() . Nebo např. víme, že rozdělení (doby životnosti
výrobku) má distribuční funkci
. Nebo např. víme, že rozdělení (doby životnosti
výrobku) má distribuční funkci
![]() , ale neznáme parametry
, ale neznáme parametry
![]() a
a ![]() . Zajímá nás nějaká charakteristika
. Zajímá nás nějaká charakteristika ![]() rozdělení, tedy
rozdělení, tedy
![]() , např.
, např.
![]() . Chceme
nalézt vhodnou statistiku výběru z náhodného rozdělení
. Chceme
nalézt vhodnou statistiku výběru z náhodného rozdělení
![]() , která dobře aproximuje
, která dobře aproximuje ![]() .
.
Definujeme
|
|
náhodný výběr z rozdělení
|
|
|
vektor z k-rozměrného prostoru neznámých parametrů |
|
|
charakteristika rozdělení - funkce
|
|
|
bodový odhad |
Nestranný (nevychýlený) odhad
![\begin{displaymath}\forall \vec{\theta} \in \Omega \ \ \ \ \ \ \ \ \ \ \ \
E\left[ T(\vec{X}) \right] = \tau (\vec{\theta}) \end{displaymath}](img127.gif)
Vychýlení odhadu
![\begin{displaymath}B(\vec{\theta}) = E\left[ T(\vec{X})\right] - \tau (\vec{\theta}) \end{displaymath}](img128.gif)
Nejlepší nestranný odhad ![]()
![\begin{displaymath}\forall T^*(\vec{X}) \ {\rm nestranné} \ \ \ \ \ \ \ \ \ \ \ \
D\left[ T^*(\vec{X}) \right] \ge D\left[ T(\vec{X}) \right] \end{displaymath}](img130.gif)
Pozn. Není zaručena ![]() nejlepšího nestranného odhadu.
Není vždy třeba trvat na nestrannosti odhadu.
nejlepšího nestranného odhadu.
Není vždy třeba trvat na nestrannosti odhadu.
Střední kvadratická chyba odhadu
![\begin{displaymath}E \left[ \left( T(\vec{X}) - \tau (\vec{\theta}) \right)^2 \right] =
D\left[ T(\vec{X}) \right] + B^2(\vec{\theta})\end{displaymath}](img132.gif)
Pozn. To ovšem neznamená, že vychýlený odhad vždy musí
mít větší střední kvadratickou chybu než odhad nevychýlený. Např.
![]() je nevychýlený odhad rozptylu
je nevychýlený odhad rozptylu ![]() a
a ![]() je vychýlený odhad
s vychýlením
je vychýlený odhad
s vychýlením
![]() . Střední kvadratická chyba
odhadu
. Střední kvadratická chyba
odhadu ![]() je pro výběry z normálního rozdělení větší než u odhadu
je pro výběry z normálního rozdělení větší než u odhadu
![]()
![\begin{displaymath}E \left[ (S^2 - \sigma^2)^2 \right] = \frac{2 \sigma^4}{n-1} >
E \left[ (M_2 - \sigma^2)^2 \right] = \frac{2n-1}{n^2}\sigma^4 \end{displaymath}](img136.gif)
Asymptotické vlastnosti odhadů
Asymptoticky nestranný odhad
![\begin{displaymath}\forall \vec{\theta} \in \Omega \ \ \ \ \ \ \ \ \ \ \ \
\lim_{n \rightarrow \infty} E[T_n(\vec{X})] = \tau (\vec{\theta}) \end{displaymath}](img137.gif)
Konzistentní odhad - Pokud pro odhad platí, že
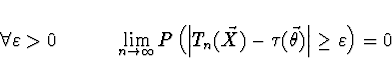
Věta Nechť je odhad ![]() asymptotický nestranný a nechť
jeho rozptyl jde k 0
asymptotický nestranný a nechť
jeho rozptyl jde k 0
(
![]() ),
pak je odhad konzistentní.
),
pak je odhad konzistentní.
Důkaz Z předpokladů vyplývá, že
![]() existuje
existuje
![]() takové, že
takové, že
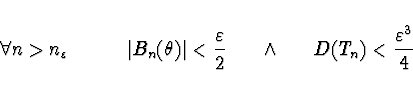
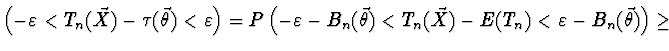 |
|||
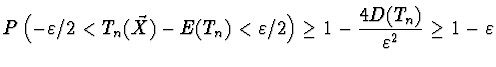 |