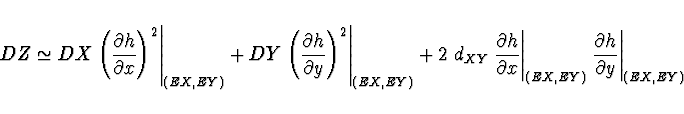Nechť je dána lineární funkce
![]() (
(![]() jsou
konstanty). Pak
jsou
konstanty). Pak
Nechť jsou náhodné veličiny ![]() ,
, ![]() nezávislé,
nechť
nezávislé,
nechť
![]() . Pak charakteristická funkce
. Pak charakteristická funkce
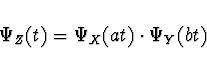
Pro obecnou funkci ![]() je distribuční funkce
náhodné veličiny
je distribuční funkce
náhodné veličiny ![]() dána vztahem
dána vztahem
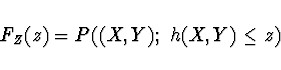
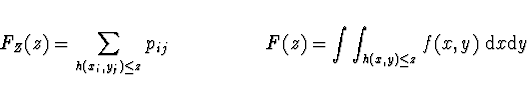
Vzájemně jednoznačné zobrazení z
![]() je dáno předpisem
je dáno předpisem ![]() ,
, ![]() . Existuje tedy
inverzní zobrazení
. Existuje tedy
inverzní zobrazení
![]() ,
,
![]() .
Pokud pro daný bod
.
Pokud pro daný bod ![]() existuje Jacobián
existuje Jacobián
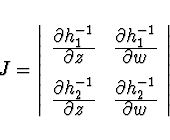
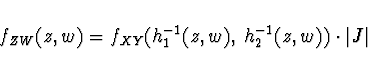
Přibližné stanovení charakteristik funkce
náhodného vektoru
Nechť je dána funkce ![]() . Nechť jsou známy
. Nechť jsou známy ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() a nechť
a nechť ![]() ,
, ![]() . Pokud nejsou k dispozici
žádné jiné informace, pak lze přibližně odhadnout
. Pokud nejsou k dispozici
žádné jiné informace, pak lze přibližně odhadnout
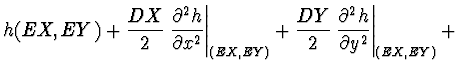 |
|||
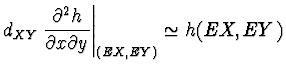 |