Bernoulliova věta - Nech» ![]() je veličina
s alternativním rozdělením (0,1) s pravděpodobností
je veličina
s alternativním rozdělením (0,1) s pravděpodobností ![]() . Nech»
je provedeno
. Nech»
je provedeno ![]() po dvou vzájemně nezávislých pokusů a nech»
po dvou vzájemně nezávislých pokusů a nech»
![]() . Pak pro
. Pak pro
![]() je
je
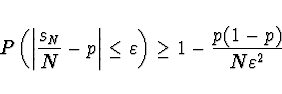
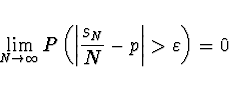
Čebyąevova věta - Nech» ![]() je posloupnost po 2 navzájem nezávislých náhodných veličin se středními
hodnotami
je posloupnost po 2 navzájem nezávislých náhodných veličin se středními
hodnotami ![]() a s disperzemi
a s disperzemi ![]() . Pak
. Pak
![]()
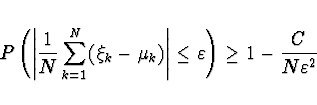
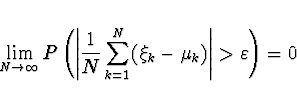
Centrální limitní teorém - Nech» po 2 navzájem
nezávislé náhodné veličiny ![]() mají stejná rozdělení se střední hodnotou
mají stejná rozdělení se střední hodnotou
![]() a rozptylem
a rozptylem
![]() . Pak pro
. Pak pro
![]() se rozdělení veličiny
se rozdělení veličiny
![]() blíľí
normálnímu rozdělení
blíľí
normálnímu rozdělení
![]() se střední hodnotou
se střední hodnotou ![]() a rozptylem
a rozptylem
![]() .
.