Příklady rozdělení náhodného vektoru

Multinomické rozdělení - Nechť náhodný pokus má $n$ možných výsledků s pravděpodobností $p_i,\ i=1,2,\dots,n$ ( $\sum_{i=1}^n p_i = 1$). Pak pravděpodobnost, že z $N$ pokusů dojde $x_i$-krát k i-tému výsledku je dána multinomickým rozdělením

$$p(x_1,x_2,\dots,x_n) = \frac{N!}{x_1! x_2! \dots x_n!} p_1^{x_1} p_2^{x_2}\dots p_n^{x_n}$$

kde $\sum_{k=1}^n x_k = N$.

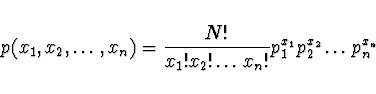
2D normální rozdělení - Nechť $\mu_X$, $\mu_Y$, $\sigma_X$, $\sigma_Y$ jsou střední hodnoty a směrodatné odchylky veličin $X$, $Y$ a nechť $\rho$ je jejich lineární korelační koeficient ($\vert \rho \vert < 1$). Pak sdružená hustota pravděpodobnosti je

$$f(x,y) = \frac{1}{2 \pi \sigma_X \sigma_Y \sqrt{1 - \rho^2}} \ \exp \left( -\, \frac{Q(x,y)}{2} \right)$$

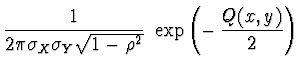$$Q(x,y) = \frac{1}{1 - \rho^2} \left[ \frac{(x-\mu_X)^2}{\sigma_X^2} + \fra... ...^2}{\sigma_Y^2} - 2 \rho\, \frac{(x-\mu_X)(y-\mu_Y)}{\sigma_X \sigma_Y} \right]$$

U tohoto rozdělení plyne z nekorelovanosti nezávislost.