


Next: Příklady rozdělení náhodného vektoru
Up: Náhodný vektor
Previous: Rozdělení náhodného vektoru
Obecné a centrální momenty - Kromě momentů
náhodných veličin
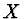 ,
, 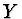 jsou ještě definovány smíšené momenty, např. smíšený počáteční
moment
jsou ještě definovány smíšené momenty, např. smíšený počáteční
moment
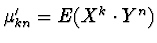 . Z počátečních momentů
jsou nejpoužívanější střední hodnoty
. Z počátečních momentů
jsou nejpoužívanější střední hodnoty 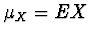 a
a 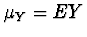 ,
z centrálních momentů rozptyly
,
z centrálních momentů rozptyly 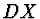 a
a 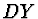 .
.
Kovariance - smíšený centrální moment 2. řádu
- nejjednodušší charakteristika souvislosti 2 náhodných veličin
Kovariance kladná - se zvětšením 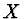 se pravděpodobně zvětší i
se pravděpodobně zvětší i 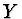 .
.
Kovariance záporná - se zvětšením 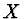 se pravděpodobně
se pravděpodobně 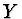 zmenší.
zmenší.
Kovarianční matice
Matice centrálních momentů 2. řádu - na diagonále rozptyl, mimo
kovariance, v této souvislosti se někdy označuje
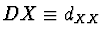 .
.
Lineární korelační koeficient
Je-li 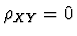 , náhodné veličiny
, náhodné veličiny 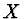 ,
, 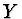 jsou
nekorelované. Veličiny nezávislé jsou
nekorelované, naopak to platit nemusí.
jsou
nekorelované. Veličiny nezávislé jsou
nekorelované, naopak to platit nemusí.
Platí
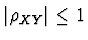 . Dále
. Dále
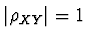 právě tehdy,
jestliže jsou náhodné veličiny
právě tehdy,
jestliže jsou náhodné veličiny 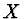 ,
, 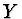 lineárně závislé, tj.
lineárně závislé, tj.
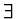 konstanty
konstanty
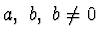 takové, že
takové, že 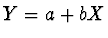 .
.
Charakteristická funkce



Next: Příklady rozdělení náhodného vektoru
Up: Náhodný vektor
Previous: Rozdělení náhodného vektoru
Jiri Limpouch
2000-11-02
![]() ,
, ![]() jsou ještě definovány smíšené momenty, např. smíšený počáteční
moment
jsou ještě definovány smíšené momenty, např. smíšený počáteční
moment
![]() . Z počátečních momentů
jsou nejpoužívanější střední hodnoty
. Z počátečních momentů
jsou nejpoužívanější střední hodnoty ![]() a
a ![]() ,
z centrálních momentů rozptyly
,
z centrálních momentů rozptyly ![]() a
a ![]() .
.
![\begin{displaymath}\mu_{11} = E\left[ (X - EX)(Y-EY) \right] \equiv d_{XY}
\equiv {\rm Cov}(X,Y)\ \ .\end{displaymath}](img259.gif)
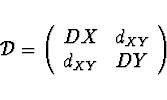
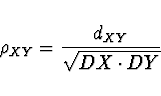
![\begin{displaymath}\Psi_{XY} (t_1,t_2) = E\left[ \exp (it_1x + it_2y) \right] \end{displaymath}](img268.gif)