Rozdělení náhodného vektoru

Sdružená distribuční funkce náhodných veličin $X,\; Y$ je definována předpisem

$$F(x,y) = P(X \le x,\; Y \le y)$$

Sdružená distribuční funkce má obdobné vlastnosti jako distribuční funkce v jedné proměnné. Pravděpodobnost, že náhodný vektor je z obdélníkové oblasti lze vyjádřit pomocí distribuční funkce

$$P(x_1 < X \le x_2,\; y_1 < Y \le y_2) = F(x_2,y_2) - F(x_2,y_1) - F(x_1,y_2) + F(x_1,y_1)$$

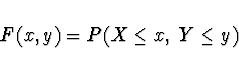
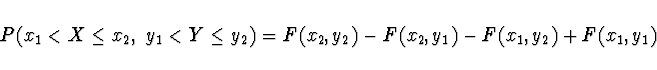
Jestliže existuje nejvýše spočetně mnoho hodnot náhodného vektoru, jde o náhodný vektor s diskrétním rozdělením a sdružená distribuční funkce

$$F(x,y) = \sum_{(i,j),\ x_i \le x,\; y_j \le y} p_{ij}$$

Veličina $p_{ij}$ se nazývá sdružená pravděpodobnostní funkce.

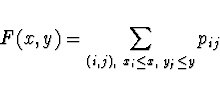
Distribuční funkce $F(x,y)$ je absolutně spojitá, pokud $\exists$ funkce $f(x,y) \ge 0$ ( sdružená hustota pravděpodobnosti) taková, že

$$F(x,y) = \int_{-\infty}^x \int_{-\infty}^y f(x',y')\; {\rm d}x' {\rm d}y'$$

Pokud $\exists$ druhá smíšená derivace distribuční funkce, pak

$$f(x,y) = \frac{\partial^2}{\partial x\; \partial y} F(x,y)$$

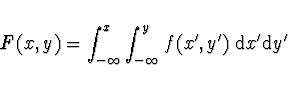
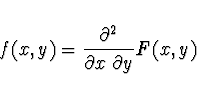
Distribuční funkce složky $X$ (resp. $Y$) náhodného vektoru -
marginální distribuční funkce

$$F_X (x) = P (X \le x) = \lim_{y \rightarrow \infty} F(x,y)$$

$$F_Y (y) = P (Y \le y) = \lim_{x \rightarrow \infty} F(x,y)$$

Podobně lze definovat marginální pravděpodobnostní funkce či marginální hustoty pravděpodobnosti. Jde vlastně o příslušné funkce náhodné veličiny.

Nezávislost Náhodné veličiny $X$, $Y$ jsou nezávislé právě tehdy, jestliže

$$F(x,y) = F_X (x) \cdot F_Y(y)$$

Pro náhodný vektor s diskrétním (resp. spojitým) rozdělením platí, že náhodné veličiny $X$, $Y$ jsou nezávislé právě tehdy, jestliže

$$p_{ij} = q_i \cdot r_j \ \ \ \ \ \ \ \ \ \ f(x,y) = f_X (x) \cdot f_Y (y)$$

kde $q_i$, $r_j$ jsou marginální pravděpodobnostní funkce diskrétních veličin $X$, $Y$ ($f_X$, $f_Y$ jsou marginální hustoty pravděpodobnosti).

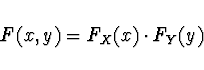
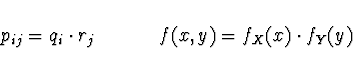
Korelační tabulka Pravděpodobnostní funkce diskrétního náhodného vektoru s konečným počtem hodnot se často prezentuje pomocí korelační tabulky, kde kromě sdružené pravděpodobnostní funkce jsou v posledním řádku (sloupci) uvedeny marginální distribuční funkce (součty sloupců, resp. řádků).

x $\backslash$ y	$y_1$	$y_2$	...	$y_m$	$\sum_j p_{ij}$
$x_1$	$p_{11}$	$p_{12}$	...	$p_{1m}$	$q_1$
$x_2$	$p_{21}$	$p_{22}$	...	$p_{2m}$	$q_2$
			...
$x_n$	$p_{n1}$	$p_{n2}$	...	$p_{nm}$	$q_n$
$\sum_i p_{ij}$	$r_1$	$r_2$	...	$r_m$	1

Marginální pravděpodobnosti $X$, $Y$ jsou $q_i$, $r_j$.

Podmíněná pravděpodobnost (hustota pravděpodobnosti) je definována pro náhodný vektor s diskrétním (spojitým) rozdělením

$$p(x_i \vert y_j) = \frac{p_{ij}}{r_j} \ \ \ \ \ \ \ \ \ \ \ \... ... \ \ \ \ \ \ \ \ \ \ \ \ f(x \vert y) = \frac{f(x,y)}{f_Y (y)}$$