Stejnoměrné rozdělení má konstantní hustotu pravděpodobnosti v nějakém intervalu
Stejnoměrné rozdělení
Stejnoměrné rozdělení má konstantní hustotu pravděpodobnosti v nějakém
intervalu ![]() a nulovou hustotu pravděpodobnosti mimo něj
a nulovou hustotu pravděpodobnosti mimo něj
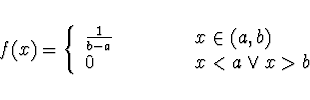
Normální (Gaussovo) rozdělení
Hustota pravděpodobnosti je pro normální rozdělení o střední hodnotě
![]() a směrodatné odchylce
a směrodatné odchylce
![]() dána vztahem
dána vztahem
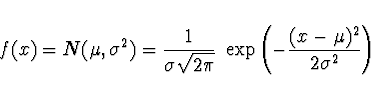
Distribuční funkce pro normální rozdělení ![]()
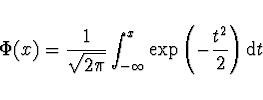
Distribuční funkce pro normální rozdělení
![]()
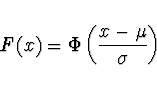
Většinou není tabelována ![]() , ale je tabelována chybová
funkce
, ale je tabelována chybová
funkce ![]()
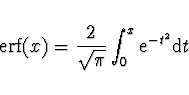
![\begin{displaymath}
\Phi (x) = \frac{1}{2} \left[ 1 + {\rm erf}
\left( \frac{x}{ \sqrt{2} } \right) \right]
\end{displaymath}](img165.gif)
Charakteristická funkce normálního rozdělení je
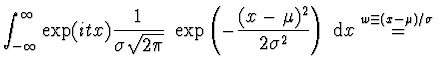 |
|||
![$\displaystyle \exp (i\mu t - \sigma^2 t^2/2)
\underbrace{\frac{1}{\sqrt{2 \pi}}...
... - i \frac{\sigma t}{\sqrt{2}}
\right)^2 \right] {\rm d}w }_{\displaystyle 1} =$](img167.gif) |
|||