Reálná funkce ![]() náhodné veličiny je opět
náhodnou veličinou.
náhodné veličiny je opět
náhodnou veličinou.
Nechť funkce ![]() je rostoucí (klesající) funkce.
Pak existuje inverzní funkce
je rostoucí (klesající) funkce.
Pak existuje inverzní funkce
![]() .
Distribuční funkce
.
Distribuční funkce ![]() je dána vztahy
je dána vztahy
 |
|||
 |
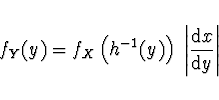
Pro obecnou funkci ![]() je distribuční funkce
je distribuční funkce ![]() náhodné
veličiny
náhodné
veličiny ![]() je pro případ
diskrétní (resp. spojité) náhodné veličiny X definována
následujícími vztahy
je pro případ
diskrétní (resp. spojité) náhodné veličiny X definována
následujícími vztahy
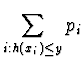 |
|||
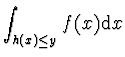 |
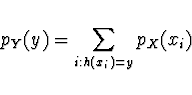
Nechť existuje konečný počet ![]() takových, že
takových, že ![]() .
Nechť pro
.
Nechť pro
![]() derivace
derivace
![]() .
Pak
.
Pak ![]() hustota pravděpodobnosti
hustota pravděpodobnosti ![]() náhodné veličiny
náhodné veličiny ![]()
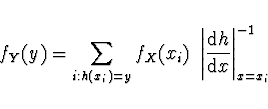
Příklad 1 Nechť veličina ![]() má stejnoměrné
rozdělení v intervalu
má stejnoměrné
rozdělení v intervalu
![]() . Jaké rozdělení má veličina
. Jaké rozdělení má veličina
![]() ?
?
Je tedy
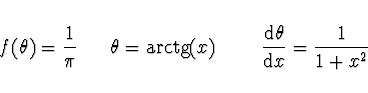

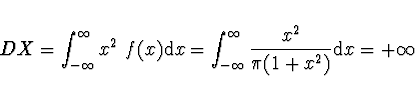
Příklad 2 Nechť veličina X má normální rozdělení
![]() . Jaké rozdělení má veličina
. Jaké rozdělení má veličina ![]() ?
?
Inverzní funkce existuje pro
nezáporná (nekladná)
![]() .
Zde
.
Zde
![]() . Pak hustota pravděpodobnosti
veličiny
. Pak hustota pravděpodobnosti
veličiny ![]() je
je
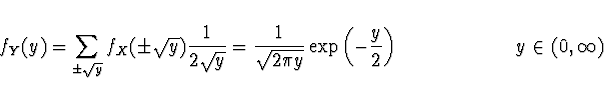
Přibližné stanovení charakteristik funkce
náhodné veličiny
V praxi je někdy k dispozici pouze jediná změřená hodnota veličiny ![]() (odhad její střední hodnoty) a směrodatná odchylka měření
(odhad její střední hodnoty) a směrodatná odchylka měření ![]() (daná například udanou chybou měřícího přístroje). Pokud je variační
koeficient
(daná například udanou chybou měřícího přístroje). Pokud je variační
koeficient ![]() , lze přibližně odhadnout charakteristiky
veličiny
, lze přibližně odhadnout charakteristiky
veličiny ![]() . Předpokládejme, že veličina X je spojitá
. Předpokládejme, že veličina X je spojitá
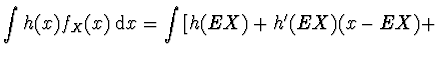 |
|||
![$\displaystyle \left. \frac{h''(EX)}{2} (x-EX)^2 + \dots \right]\,
f_X (x)\; {\rm d}x \simeq h(EX) + \frac{h''(EX)}{2} DX \simeq h(EX)$](img207.gif) |
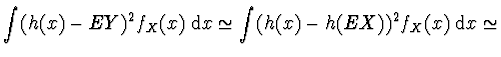 |
|||
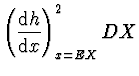 |