Nechť jsou pouze 2 možné výsledky náhodného pokusu - událost nastane (1) nebo událost nenastane (0). Označme
Alternativní rozdělení
Nechť jsou pouze 2 možné výsledky náhodného pokusu - událost nastane (1) nebo
událost nenastane (0). Označme ![]() pravděpodobnost výsledku 1,
pravděpodobnost výsledku 0 je pak
pravděpodobnost výsledku 1,
pravděpodobnost výsledku 0 je pak ![]() .
Pravděpodobnostní funkce je pak
.
Pravděpodobnostní funkce je pak
![]() , kde
, kde ![]() .
.
Binomické rozdělení ![]()
Rozdělení počtu úspěšných pokusů při provedení ![]() navzájem nezávislých
pokusů se stejným alternativním rozdělením
navzájem nezávislých
pokusů se stejným alternativním rozdělením
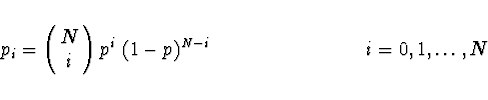
Střední hodnota
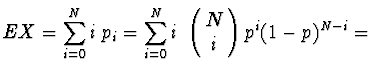 |
|||
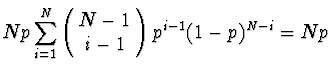 |
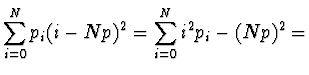 |
|||
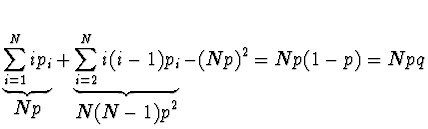 |
 |
|||
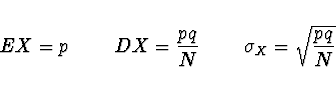
Hypergeometrické rozdělení
Soubor ![]() výrobků obsahuje
výrobků obsahuje ![]() vadných výrobků. Při statistické přejímce
je vybráno
vadných výrobků. Při statistické přejímce
je vybráno ![]() . Pak pravděpodobnost, že
. Pak pravděpodobnost, že
![]() výrobků
bude vadných je
výrobků
bude vadných je
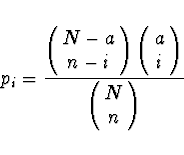
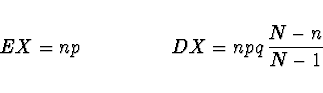
Poissonovo rozdělení
Počet událostí v daném intervalu ![]() vyhovuje Poissonovu rozdělení,
pokud platí
vyhovuje Poissonovu rozdělení,
pokud platí
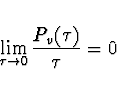

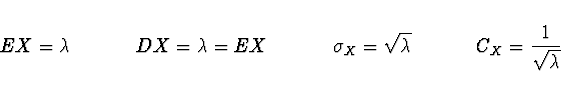
![\begin{displaymath}\Psi (t) = \exp [ \lambda ({\rm e}^{it} - 1) ] \end{displaymath}](img144.gif)
Poissonovo rozdělení se často objevuje ve fyzikální praxi - počet
částic zaregistrovaných čítačem, počet krvinek v políčku mikroskopu
(délkou intervalu je plocha políčka).
Poissonovo rozdělení je limitou binomického rozdělení pro
![]() a
a
![]() .
.