


Next: Některá diskrétní rozdělení
Up: Náhodná veličina (jednorozměrná reálná)
Previous: Momenty rozdělení
Jiným způsobem
zápisu náhodné veličiny je její charakteristická funkce (jde vlastně o
Fourierovu transformaci hustoty pravděpodobnosti)
kde 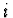 je komplexní jednotka. Pro diskrétní a spojitou náhodnou veličinu
je tak charakteristická funkce dána vztahy
je komplexní jednotka. Pro diskrétní a spojitou náhodnou veličinu
je tak charakteristická funkce dána vztahy
Charakteristická funkce 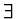 pro
pro 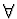 náhodné veličiny.
Rozdělení náhodné veličiny je charakteristickou funkcí jednoznačně
určeno.
náhodné veličiny.
Rozdělení náhodné veličiny je charakteristickou funkcí jednoznačně
určeno.
Nechť existuje prvních 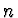 obecných momentů
obecných momentů
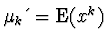 ,
,
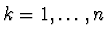 . Pak charakteristická funkce má prvních
. Pak charakteristická funkce má prvních 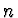 derivací
v bodě
derivací
v bodě 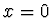 daných vztahem
daných vztahem
Pak má prvních 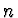 členů Taylorova rozvoje charakteristické funkce náhodné
veličiny tvar
členů Taylorova rozvoje charakteristické funkce náhodné
veličiny tvar
Pokud provedeme substituci 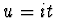 , pak funkci
, pak funkci
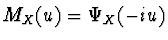 nazýváme momentovou vytvořující funkcí.
nazýváme momentovou vytvořující funkcí.
Momentová vytvořující funkce existuje pouze pokud má náhodná veličina
konečné obecné momenty všech řádů.
Jiri Limpouch
2000-11-02
![\begin{displaymath}
\Psi_X (t) = {\rm E} \left[ \exp (i t x) \right]
\end{displaymath}](img95.gif)
![\begin{displaymath}
\Psi_X (t) = {\rm E} \left[ \exp (i t x) \right]
\end{displaymath}](img95.gif)
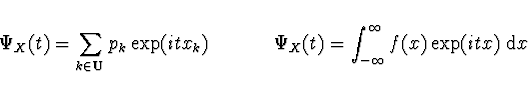
![]() obecných momentů
obecných momentů
![]() ,
,
![]() . Pak charakteristická funkce má prvních
. Pak charakteristická funkce má prvních ![]() derivací
v bodě
derivací
v bodě ![]() daných vztahem
daných vztahem
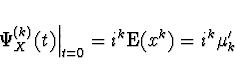
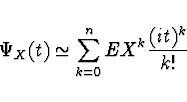
![\begin{displaymath}
M_X (u) = {\rm E} \left[ \exp (u x) \right] =
\sum_{k=0}^\infty EX^k \frac{(u)^k}{k!}
\end{displaymath}](img108.gif)