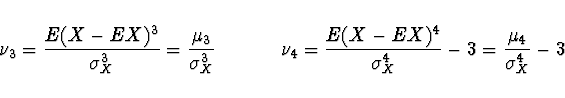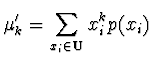 |
|||
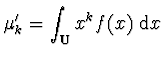 |
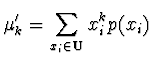 |
|||
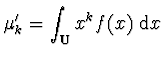 |
Centrální momenty - K-tý centrální (středový) moment
![]() náhodné veličiny
náhodné veličiny ![]() je dán
je dán
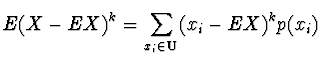 |
|||
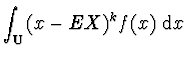 |
Rozptyl (disperze) ![]() je druhý centrální moment
je druhý centrální moment ![]() náhodné veličiny
náhodné veličiny ![]() .
.
Směrodatná odchylka
![]() je mírou šířky
rozdělení.
je mírou šířky
rozdělení.
Variační koeficient
![]() je mírou relativní
šířky rozdělení.
je mírou relativní
šířky rozdělení.
Věta (Čebyševova nerovnost) Nechť náhodná veličina ![]() má konečný rozptyl. Pak
má konečný rozptyl. Pak
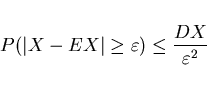
Koeficient šikmosti ![]() a
koeficient špičatosti
a
koeficient špičatosti ![]() jsou definovány
jsou definovány