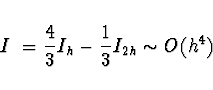Praktická implementace složeného lichoběžníkového pravidla

Podintervaly při jednotlivých voláních lichoběžníkového pravidla

Postup přidávání bodů - hodnoty proměnných NV, NS, N a ND:

volání NV	počet subintervalů NS	počet bodů N	počet přidaných bodů ND
1	1	2	0
2	2	3	1
3	4	5	2
4	8	9	4

Pro začátek integrace ${\tt NV} = 1$, je algoritmus

Int := (b - a) / 2 * (f(a) + f(b));
ND := 1;

Pro volání ${\tt NV} = k > 1$ je algoritmus

HD := (b - a) / ND;
SUM := 0; x := a + 0.5 * HD;
for j := 1 to ND do
   begin
      SUM := SUM + f(x);
      x := x + HD
   end;
Int := 0.5 * (Int + (b - a) * SUM / ND);
ND := 2 * ND;

Postupné zpřesňování při jednotlivých voláních odpovídá půlení podintervalů.
Přitom se využije předchozích bodů.
Odhad chyby získáme porovnáním výsledků pro $h$ a $h/2$.

Odhad chyby pro rozšířené lichoběžníkové pravidlo.

Chyba je funkcí jen sudých mocnin $1/N$. Chyba je dána okrajem

$$\int \limits_{x_1}^{x_N} = h \left[ \frac{1}{2} f_1 + f_2 + f_3 + \dots + f_{N-1} + \frac{1}{2} f_N \right] - \frac{B_2 h^2}{2!} \left( f'_N - f'_1 \right) - \dots -$$

$$- \frac{B_{2k} h^{2k}}{(2k)!} \left( f_N^{(2k-1)} - f_1^{(2k-1)} \right) - \dots$$

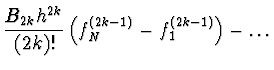V předchozím vztahu jsou $B_k$ Bernoulliova čísla, pro která platí $B_0 = 1$, $B_2 = 1/6$, $B_4 = -1/30$, $B_6 = 1/42$, $B_8 = - 1/30$, $B_{10} = 5/66$ a $B_{12} = - 691/2730$. Rozvoj nemusí konvergovat, jde o asymptotický rozvoj. Chyby rozvoje můžeme odhadnout shora dvojnásobkem absolutní hodnoty nejnižšího zanedbaného členu.

Zpřesnění výsledku

$$I~= \frac{4}{3} I_h - \frac{1}{3} I_{2h} \sim O(h^4)$$

Výsledek je zpřesněn ze dvou následujících výsledků integrační procedury. Tento výsledek je identický se složeným Simpsonovým pravidlem.