Polynom ![]() -tého stupně
-tého stupně
![]() má logaritmus
má logaritmus
![]() .
Definujeme
.
Definujeme
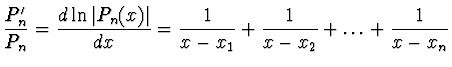 |
|||
![$\displaystyle \left[ \frac{P'_n}{P_n} \right]^2 - \frac{P''_n}{P_n} = -
\frac{d...
...vert P_n(x)\vert}{dx^2} = \frac{1}{(x - x_1)^2} +
\dots + \frac{1}{(x - x_n)^2}$](img135.gif) |
Nyní ![]() a
a ![]() vyjádříme tak, že pro kořen
vyjádříme tak, že pro kořen ![]() nejbližší k
nejbližší k ![]() ,
položíme
,
položíme
![]() a pro ostatní
kořeny
a pro ostatní
kořeny ![]() předpokládáme, že
předpokládáme, že
![]() . Potom
. Potom
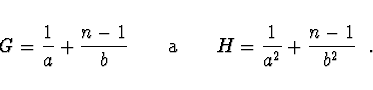
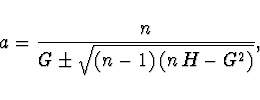
Pozn. I při hledání reálných kořenů můžeme při využití
této metody dostat komplexní mezivýsledky.
Pozn. Existuje ryze reálná metoda na výpočet reálných kořenů pomocí rozkladu na kvadratické polynomy ( Bairstowova metoda).