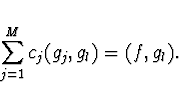

Next: Spojitý případ
Up: Aproximace metodou nejmenších čtverců
Previous: Aproximace metodou nejmenších čtverců
Ve statistice je často třeba aproximovat naměřená
data, zatížená náhodnými chybami měření nebo náhodným šumem
funkční závislostí. Uvedená závislost je nazývána modelem, který
je znám až na  neznámých parametrů.
V matematické statistice je uvedená úloha nazývána regresí, a k jejímu
řešení se často používá metoda nejmenších čtverců.
Hlavním cílem statistické analýzy je
neznámých parametrů.
V matematické statistice je uvedená úloha nazývána regresí, a k jejímu
řešení se často používá metoda nejmenších čtverců.
Hlavním cílem statistické analýzy je
- vypočítat koeficienty
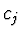 , kde
, kde
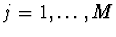
- určit směrodatné odchylky koeficientů
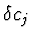 , kde
, kde
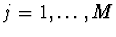
- zjistit kvalitu modelu (zda je použitý model statisticky přijatelný)
Zde chceme nalézt vhodnou aproximaci. Úlohou může být nalezení
hladké aproximace bez konstrukce modelu.
Jednou z možností je použít zvonové spliny jako
bázové funkce.
Nechť je dána síť bodů k krokem 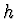 . Konstruujeme
zvonový spline (bell spline, B-spline) se středem v
. Konstruujeme
zvonový spline (bell spline, B-spline) se středem v 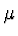 . Označme
. Označme
potom je zvonový spline 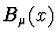 dán vztahy
dán vztahy
Zvonový spline je funkce třídy 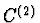 nenulová pouze v intervalu
nenulová pouze v intervalu
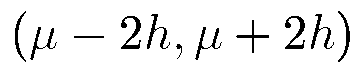 . Hledání koeficientů u zvonových splinů vede
na úlohu řešení systému lineárních rovnic s pásovou maticí.
. Hledání koeficientů u zvonových splinů vede
na úlohu řešení systému lineárních rovnic s pásovou maticí.
Výpočet parametrů lineární aproximace metodou nejmenších čtverců
- Položíme
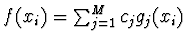 , kde
, kde 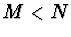 ,
a získáme tak
,
a získáme tak 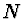 rovnic pro
rovnic pro 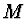 neznámých koeficientů
neznámých koeficientů 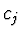 .
Ve smyslu nejmenších čtverců úlohu řeší SVD metoda.
.
Ve smyslu nejmenších čtverců úlohu řeší SVD metoda.
- Funkce
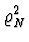 má minimum, pokud pro
má minimum, pokud pro
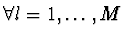 platí
platí
Řešíme pak soustavu 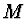 lineárních rovnic o
lineárních rovnic o 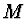 neznámých
neznámých 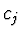 nazývanou normální rovnice.
nazývanou normální rovnice.
Pozn. Jestliže definujeme skalární součin
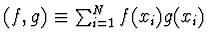 ,
pak lze soustavu normálních rovnic přepsat do tvaru
,
pak lze soustavu normálních rovnic přepsat do tvaru
Výběr bázových (základních) funkcí
- Polynomy - jako bázové funkce jsou často voleny
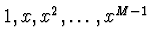 . Tyto základní funkce jsou však vhodné
jen pro malá
. Tyto základní funkce jsou však vhodné
jen pro malá 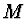 , protože při větších M jsou tyto polynomy
přibližně rovnoběžné, soustava normálních rovnic je špatně
podmíněná a chyba koeficientů
, protože při větších M jsou tyto polynomy
přibližně rovnoběžné, soustava normálních rovnic je špatně
podmíněná a chyba koeficientů 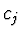 je značná.
je značná.
- Ortogonalizované polynomy - problémy, které vznikají
v předchozím případě, zde odpadají. Tyto polynomy konstruujeme
Gramm-Schmidtovým ortogonalizačním procesem.
- Trigonometrické polynomy - mají základní funkce
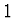 ,
,
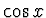 ,
, 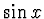 ,
, 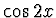 ,
, 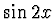 , .... Jsou ortogonální
pro všechny body
, .... Jsou ortogonální
pro všechny body
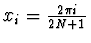 , kde
, kde
 .
.


Next: Spojitý případ
Up: Aproximace metodou nejmenších čtverců
Previous: Aproximace metodou nejmenších čtverců
Jiri Limpouch
2000-03-24
![]() neznámých parametrů.
V matematické statistice je uvedená úloha nazývána regresí, a k jejímu
řešení se často používá metoda nejmenších čtverců.
Hlavním cílem statistické analýzy je
neznámých parametrů.
V matematické statistice je uvedená úloha nazývána regresí, a k jejímu
řešení se často používá metoda nejmenších čtverců.
Hlavním cílem statistické analýzy je
![]() . Konstruujeme
zvonový spline (bell spline, B-spline) se středem v
. Konstruujeme
zvonový spline (bell spline, B-spline) se středem v ![]() . Označme
. Označme
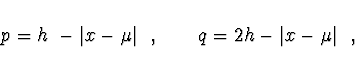

![\begin{displaymath}
\frac{\partial}{\partial c_l} \left[ \sum_{i=1}^N \left( f(x_i) -
\sum_{j=1}^M c_j g_j (x_i) \right)^2 \right] = 0.
\end{displaymath}](img288.gif)
![]() ,
pak lze soustavu normálních rovnic přepsat do tvaru
,
pak lze soustavu normálních rovnic přepsat do tvaru