

Next: Sturmova věta
Up: Kořeny polynomů
Previous: Kořeny polynomů
Nechť 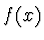 je polynom ve tvaru
je polynom ve tvaru
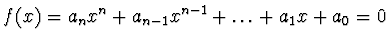 , kde
, kde 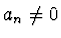 .
.
Ohraničení kořenů polynomů:
- Všechny kořeny jsou v mezikruží
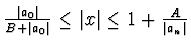 , kde pro
, kde pro 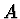 a
a 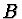 platí
platí
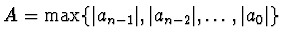 a
a
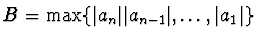 .
.
- Dále nechť
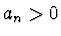 a
a 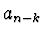 je první záporný
koeficient, platí pro všechna
je první záporný
koeficient, platí pro všechna 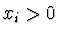 , že
, že
![$x_i < R = 1 +
\sqrt[k]{\frac{A}{a_n}}$](img77.gif) , kde
, kde
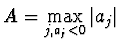 .
.
Druhé ohraničení lze po substitucích využít i k dalším odhadům:
- Substitucí
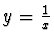 odhadneme minimální kladný
kořen.
odhadneme minimální kladný
kořen.
- Pomocí substituce
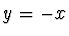 omezíme v absolutní hodnotě
největší záporný kořen.
omezíme v absolutní hodnotě
největší záporný kořen.
- Substituce
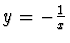 omezí v absolutní hodnotě
nejmenší záporný kořen.
omezí v absolutní hodnotě
nejmenší záporný kořen.
Jiri Limpouch
2000-04-04
![]() je polynom ve tvaru
je polynom ve tvaru
![]() , kde
, kde ![]() .
.
![$x_i < R = 1 +
\sqrt[k]{\frac{A}{a_n}}$](img77.gif) , kde
, kde