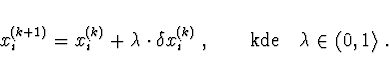Přesné řešení ![]() vyjádříme ve tvaru
vyjádříme ve tvaru
![]() . Hodnotu funkce v bodě
. Hodnotu funkce v bodě ![]() vyjádříme pomocí
Taylorovy věty
vyjádříme pomocí
Taylorovy věty
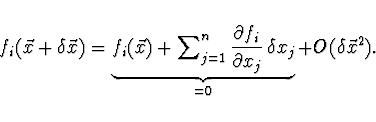
Systém rovnic linearizujeme v bodě ![]() (
(![]() -tý odhad
řešení). Máme soustavu
-tý odhad
řešení). Máme soustavu ![]() lineárních rovnic o
lineárních rovnic o ![]() neznámých
neznámých
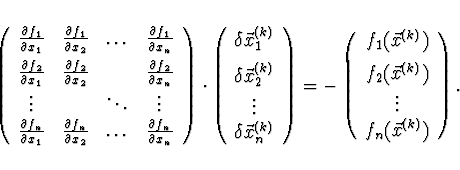
Iterační vztah je tedy
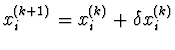 , kde
, kde
![]() .
.
Vektorově
![$\vec{x}^{(k+1)} = \vec{x}^{(k)} - \left[ Jf
\left( \vec{x}^{(k)} \right) \right]^{-1} \cdot \vec{f} \left(
\vec{x}^{(k)} \right)$](img175.gif) .
.
Při dostatečně dobrém odhadu tato metoda konverguje za velmi obecných podmínek.
V případě nutnosti počítáme derivace numericky.
Pozn. Metodu lze modifikovat tak, aby se omezení
nebezpečí příliš dlouhých kroků daleko od řešení.
V ![]() iteračních krocích chceme pokles
iteračních krocích chceme pokles
![]() .
Pokud k němu v některém kroku nedojde, místo kroku
.
Pokud k němu v některém kroku nedojde, místo kroku
![]() Newtonovy metody užijeme vztah
Newtonovy metody užijeme vztah