Prostá iterace

Soustavu (3) lze přepsat do tvaru $\vec{x} = \vec {\varphi} (\vec{x})$, tedy

$$\begin{array}{rcl} x_1 & = & \varphi_1 (\vec x), \\ x_2 & =... ...x), \\ & \vdots& \\ x_n & = & \varphi_n (\vec x). \end{array}$$

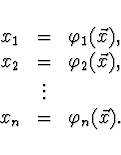
Tato soustava má stejná řešení jako soustava (3). Iterační vzorec má tvar

$$\vec{x}^{(k+1)} = \vec{\varphi} (\vec{x}^{(k)})\ \ .$$

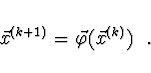
Postačující podmínka konvergence
Nechť v jistém okolí $G$ řešení $\xi$ platí, že pro $\forall \vec x \in G$ je $\vec{\varphi} (\vec x) \in G$, a $\exists q \in (0,1)$ takové, že pro $\forall \vec x, \vec y \in G$ je $\vert\vert \vec{\varphi} (\vec x) - \vec{\varphi} (\vec y) \vert\vert \leq q \vert\vert \vec x - \vec y \vert\vert$ ( kontrahující zobrazení). Pak iterační posloupnost konverguje k řešení $\xi$ a platí

$$\vert\vert \vec{x}^{(k)} - \vec{\xi} \vert\vert \leq \frac{q}{1-q} \vert\vert \vec{x}^{(k)} - \vec{x}^{(k-1)} \vert\vert \ \ .$$

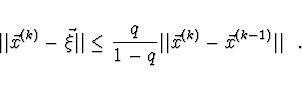
Pozn. Má-li $\vec{\varphi}$ všechny parciální derivace v okolí řešení, pak lze postačující podmínku konvergence zapsat $\vert J\varphi(x_1, x_2, \dots, x_n)\vert \leq q < 1$, kde $J$ označuje Jacobián zobrazení $\vec{\varphi}(x_1, x_2, \dots, x_n)$.

Pozn. Neexistuje žádný univerzální návod jak vhodné zobrazení $\vec{\varphi}$ sestrojit.