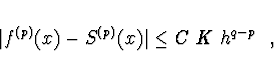Interpolační spline je lokální interpolace taková, že kromě
průchodu všemi uzlovými body ![]() má spojitou alespoň první derivaci ve
má spojitou alespoň první derivaci ve ![]() , tedy
, tedy
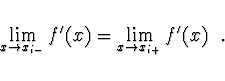
V každém subintervalu
![]() na interpolační spline
klademe čtyři podmínky (
na interpolační spline
klademe čtyři podmínky (![]() ,
, ![]() ,
,
![]() ,
,
![]() ), proto užívané
funkce musí mít alespoň 4 volitelné parametry.
), proto užívané
funkce musí mít alespoň 4 volitelné parametry.
Kubický spline používá kubické polynomy pro konstrukci
interpolačního splinu.
Okraje - zde nemá smysl mluvit o spojitosti derivací, proto
je třeba 2 podmínky dodefinovat.
Možnosti jsou
Pozn. Zadání obou dodatečných podmínek na jednom okraji by sice
zjednodušilo výpočet aproximace, ale takový algoritmus je nepoužitelný
vzhledem k numerické nestabilitě (oscilace interpolačního splinu
exponenciálně rostoucí od daného okraje).
Konstrukce kubického splinu
Druhá derivace kubický polynomu je lineární funkcí a tedy v intervalu
![]()
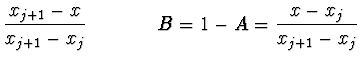 |
Po dvojím zintegrování této rovnice při uvážení podmínek
![]() dostaneme
dostaneme
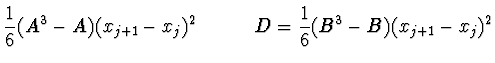 |
Derivace ![]() má tvar
má tvar
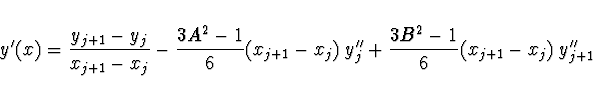
Hodnoty ![]() určíme z podmínky spojitosti první derivace
splinu
určíme z podmínky spojitosti první derivace
splinu
![]() ve tvaru
ve tvaru
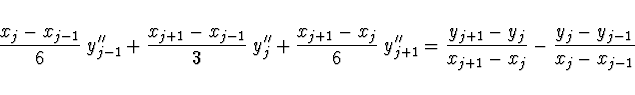
Jde tedy o soustavu lineárních rovnic pro koeficienty ![]() , kde
, kde
![]() s tridiagonální, diagonálně dominantní maticí.
Za znalosti
s tridiagonální, diagonálně dominantní maticí.
Za znalosti
![]() pak snadno určíme hodnotu splinu
pro libovolné
pak snadno určíme hodnotu splinu
pro libovolné
![]() .
.
Konvergence kubického splinu
Nechť ![]() je řádu
je řádu ![]() na intervalu
na intervalu
![]() (tedy spojité derivace až do
(tedy spojité derivace až do ![]() -té včetně), kde
-té včetně), kde
![]() . Dále nechť interval
. Dále nechť interval
![]() je rozdělen na
podintervaly délky
je rozdělen na
podintervaly délky ![]() , kde
, kde ![]() , a
, a
![]() . Mějme dále konstantu
. Mějme dále konstantu ![]() , pro kterou platí
, pro kterou platí
![]() . Je-li
. Je-li ![]() kubický interpolační spline, pak pro
kubický interpolační spline, pak pro ![]() platí
platí