

Next: Interpolační spline
Up: Interpolace a extrapolace
Previous: Interpolace racionální lomenou funkcí
Interpolace, která kromě funkčních hodnot má zadané
některé derivace.
Nechť jsou dány hodnoty funkce 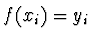 v uzlech
v uzlech 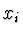 pro
pro
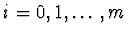 a navíc pro některé hodnoty
a navíc pro některé hodnoty 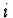 jsou dány hodnoty jejích derivací
jsou dány hodnoty jejích derivací
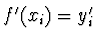 ,
,
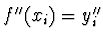 , ...,
, ...,
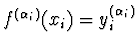 .
.
Všechny podmínky splní polynom 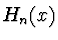 stupně
stupně
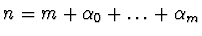 . Lze ho vyjádřit
. Lze ho vyjádřit
pomocí Lagrangeova polynomu 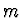 -tého stupně, který prochází všemi
uzly, a polynomu
-tého stupně, který prochází všemi
uzly, a polynomu 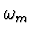 stupně
stupně 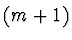 .
.
Hermitův polynom 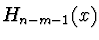 je dán tak,
aby byly splněny podmínky pro derivace v uzlech, tedy
je dán tak,
aby byly splněny podmínky pro derivace v uzlech, tedy
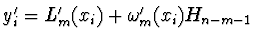 .
Odtud vyplývá, že pro
.
Odtud vyplývá, že pro
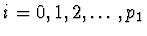 (
(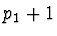 je počet
zadaných prvních derivací) platí
je počet
zadaných prvních derivací) platí
Provádíme tedy Hermiteovu interpolaci hodnot 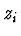 s tím, že maximální
stupeň zadané derivace je již máme o 1 nižší. Postupným opakování
uvedeného algoritmu nalezneme požadovanou interpolaci.
s tím, že maximální
stupeň zadané derivace je již máme o 1 nižší. Postupným opakování
uvedeného algoritmu nalezneme požadovanou interpolaci.
Pozn. Někdy se pod Hermiteovým interpolačním polynomem
rozumí Hermiteova interpolace v užším smyslu, kdy jsou ve
 uzlových bodech zadány hodnoty funkce a její 1. derivace.
uzlových bodech zadány hodnoty funkce a její 1. derivace.


Next: Interpolační spline
Up: Interpolace a extrapolace
Previous: Interpolace racionální lomenou funkcí
Jiri Limpouch
2000-03-24
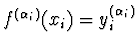 .
.
![]() v uzlech
v uzlech ![]() pro
pro
![]() a navíc pro některé hodnoty
a navíc pro některé hodnoty ![]() jsou dány hodnoty jejích derivací
jsou dány hodnoty jejích derivací
![]() ,
,
![]() , ...,
, ...,
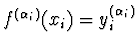 .
.
![]() stupně
stupně
![]() . Lze ho vyjádřit
. Lze ho vyjádřit
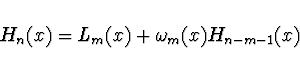
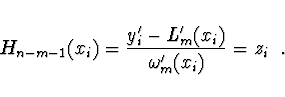
![]() uzlových bodech zadány hodnoty funkce a její 1. derivace.
uzlových bodech zadány hodnoty funkce a její 1. derivace.