Nevillův algoritmus

Hodnotu $L_n(x)$ vypočteme přesněji (byť pomaleji) pomocí Nevillova
algoritmu (používá se i termín "iterovaná interpolace").
Principem je interpolace pomocí postupně se zvětšujícího počtu uzlů. Postupná přiblížení $L_{ik}$

$$L_{ik}(x) = L_i (x, x_i, x_{i - 1}, \dots, x_{i - k}, y_i, \dots, y_{i-k})$$

jsou interpolační polynomy $k$-tého stupně. Tedy polynomy 0-tého stupně jsou $L_{i0} (x) = y_i$.

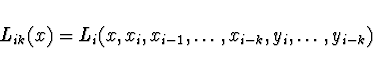
Pro polynomy platí rekurentní vztah

$$L_{ik} (x) = \frac{(x_i - x) L_{i-1,k-1} - (x_{i - 1} - x) L_{i,k-1}}{x_i - x_{i - k}}.$$

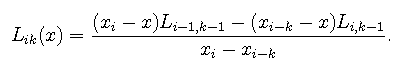
Hodnoty jednotlivých polynomů lze zapsat do tabulky ( Nevillovo schéma)

$x$	$y$	$k=0$	$k=1$	$\dots$	$k=i-1$	$k=i$	$\dots$	$k=n$
$x_0$	$y_0$	$L_{00}$
$x_1$	$y_1$	$L_{10}$	$L_{11}$
$\vdots$				$\ddots$
$x_{i-1}$	$y_{i-1}$	$L_{i-1,0}$	$L_{i-1,1}$	$\dots$	$L_{i-1,i-1}$
$x_i$	$y_i$	$L_{i,0}$	$L_{i,1}$	$\dots$	$L_{i,i-1}$	$L_{ii}$
$\vdots$							$\ddots$
$x_n$	$y_n$	$L_{n,0}$	$L_{n,1}$	$\dots$	$L_{n,i-1}$	$L_{ni}$	$\dots$	$L_{nn}$

Lagrangeův interpolační polynom $n$-tého stupně v bodě $x$ je tedy
$L_n(x) = L_{nn} (x)$.

Odhad chyby aproximace interpolačním polynomem je dán rozdílem interpolace polynomem řádu $n$ a nejlepší interpolace řádu $(n-1)$.

Praktická implementace Nevillova algoritmu, zahrnující odhad chyby využívá vztahů

$$C_{m,i} \equiv L_{i+m,m} - L_{i+m-1,m-1},$$

$$D_{m,i} \equiv L_{i+m,m} - L_{i+m,m-1},$$

$$C_{m+1,i} = \frac{(x_i - x) (C_{m,i+1} - D_{m,i})}{x_i - x_{i+m+1}},$$

$$D_{m+1,i} = \frac{(x_{i+m+1} - x) (C_{m,i+1} - D_{m,i})}{x_i - x_{i+m+1}},$$

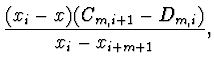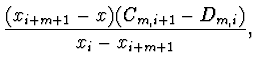V 0-tém kroku zvolíme za aproximaci $y_0 (x) = L_{0i} = y_i$ hodnotu v uzlu $x_i$ nejbližším k x, v každém dalším kroku $y_{m+1} (x) = y_m (x) + \delta y_{m+1}$, kde $\delta y_{m+1} = C_{m+1,k} \ \vee \delta y_{m+1} = D_{m+1,k}$ tak, aby se v každém kroku pokud možno symetricky rozšířila oblast použitých uzlů, $\delta y_{m+1}$ je odhad chyby interpolace v daném kroku. Nakonec vypočteme hodnotu interpolačního polynomu $y(x) = y_n (x)$ v bodě $x$ a odhad chyby této aproximace $\delta y_n$.

Hodnota chyby polynomiální interpolace je dána vztahem

$$R(x) = f(x) - L_n(x) = \omega_n(x) \frac{f^{(n+1)}(\xi)}{(n+1)!} \ \ ,$$

kde $\xi \in I \equiv \left< \min(x,x_0, \dots, x_n), \max(x, x_0, \dots, x_n) \right>$. Tuto chybu lze odhadnout

$$\vert R(x)\vert \leq \frac{\max_{\xi \in I}\ \vert f^{(n+1)}(\xi)\vert}{(n+1)!}\ \vert\omega_n(x)\vert \ .$$

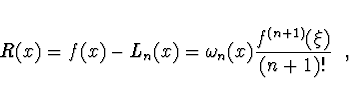
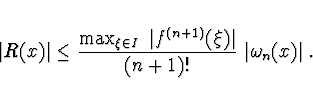
Extrapolace ( $x \not\in \left<x_0,x_n\right>$) - chyba rychle roste se zvětšováním vzdálenosti od krajního uzlu.

Vlastnosti interpolace Pro ekvidistantní uzly $x_i$ má při vyšších $n$ stupních $n$ interpolační polynom tendenci obsahovat velké oscilace mezi uzly (pokud sama funkce není polynomem). Polynomiální interpolace s ekvidistantními uzly vede obvykle k problematickým výsledkům pro $n \simeq 7$.

Konvergence Uvažuji konstantní interval $\left< a,b \right>$. Nechť počet ekvidistantních uzlů $(n+1) \rightarrow \infty$ ( $h = (b-a)/n \rightarrow 0$). Pak konvergence $L_n (x) \rightarrow f(x)$ je zaručena pro funkce analytické (mající komplexní derivaci) v celé komplexní rovině s výjimkou $\infty$. Jinak není zaručena ani bodová konvergence interpolačního polynomu k funkci.

Pozn. Pro neekvidistantní uzly může být situace lepší. Například pro
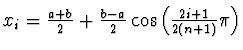$x_i = \frac{a+b}{2} + \frac{b-a}{2}\cos \left( \frac{2i+1}{2(n+1)} \pi \right)$, kde $i=0,1,\dots,n$, konverguje pro $n \rightarrow \infty$ interpolační polynom k funkci pro $\forall$ funkce třídy $C^1$ na intervalu $\langle a, b \rangle$. $\Rightarrow$ aproximace Čebyševovými polynomy