Lagrangeův interpolační polynom

Polynom $L_n$ stupně nejvýše $n$ takový, že $L_n(x_0) = y_0$, $L_n(x_1) = y_1$, ..., $L_n(x_n) = y_n$.

Uzly interpolace - body $x_0, \dots, x_n$.

Pomocné funkce $F_i (x) \ \forall i \in 0, \dots , n$ takové, že

$$F_i(x_j) = \left\{ \begin{array}{ll}1 & j=i \\ 0 & j \not= i\end{array}\right.$$

spočteme podle vztahu

$$F_i(x) = \frac{(x - x_0)(x - x_1) \dots (x-x_{i-1})(x - x_{i... ...) \dots (x_i - x_{i-1})(x_i - x_{i+1}) \dots (x_i - x_n)}\ \ .$$

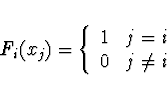
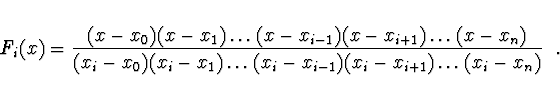
Lagrangeův interpolační polynom $n$-tého stupně má tvar

$$L_n(x) = \sum_{i=0}^n y_i\; F_i (x) = \sum_{i=0}^n y_i\; \frac{\omega_n(x)}{(x - x_i)\; \omega_n' (x_i)}\ \ ,$$

kde $\omega_n (x) = (x - x_0)(x - x_1) \dots (x - x_n)$.

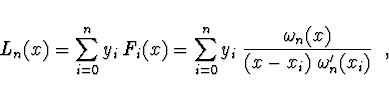
Pro ekvidistantní uzly s krokem $h = x_{i+1} - x_i$ lze užít proměnnou
$t = (x-x_0)/h$.
Lagrangeův polynom stupně $n$ lze pak zapsat

$$L_n (x) = L_n (x_0 + th) = \sum_{i = 0}^n y_i\; \frac{t(t-1) \dots (t-n)}{(t-i)\; i! (n-i)! (-1)^{n-i}}\ \ .$$

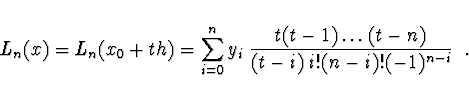
Pozn. Lagrangeův vzorec se nehodí pro numerický výpočet interpolace.

Pozn. Koeficienty interpolačního polynomu lze spočítat řešením systému lineárních rovnic. Matice tohoto systému (Van der Mondova) je však často špatně podmíněná (pro ekvidistantní uzly), vypočet koeficientů tedy není přesný.