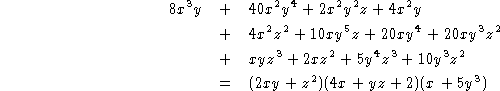


Next: Quantifier elimination
Up: Algorithms for algebraic computation
Previous: Ordinary differential equations
- consider polynomials with integer coefficients (it is simple to
convert a polynomial with rational coefficients into a problem in
this domain)
- factorization splits a given polynomial
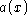 into
the product of polynomials
into
the product of polynomials 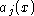 :
:

- a polynomial
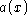 is "square free", i.e., it does
not have a factor which is the second or higher power of a
polynomial, if and only if
is "square free", i.e., it does
not have a factor which is the second or higher power of a
polynomial, if and only if 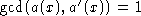 , that
is, there does not exist a polynomial other than the constant
, that
is, there does not exist a polynomial other than the constant
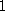 that divides the polynomial
that divides the polynomial 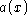 and
its derivative
and
its derivative
- if the polynomial
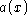 is not "square free" then
is not "square free" then

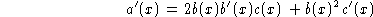
and 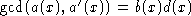
- Berlekamp algorithm for factorization of "square free" polynomials
in one variable modulo a prime
- Berlekamp-Hensel algorithm for factorization of "square free"
polynomials in one variable with integer coefficients
- Kronecker algorithm for factorization of polynomial in more variables
- these algorithms exhibit exponential complexity
- there exists algorithms with only polynomial complexity
- uses of factorization: solving of polynomial equations, integration of
rational functions, etc.
- example
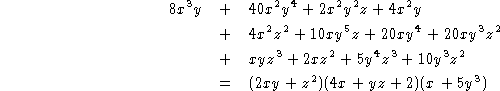
- other examples
Richard Liska
![]()
![]()
![]()
![]()
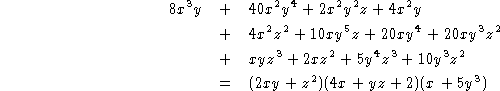
![]()
![]()
![]()
![]()