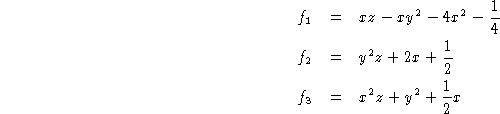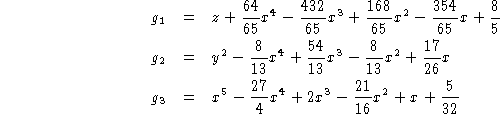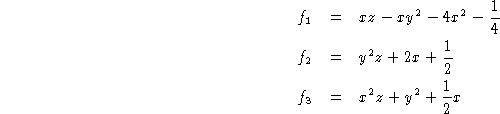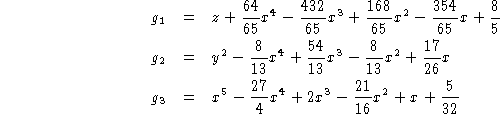


Next: Differentiation
Up: Algorithms for algebraic computation
Previous: Resultant
- solving linear systems is easy as only the inversion of a matrix
is required
- system of polynomial equations

- Grobner basis according to lexicographic ordering of variables
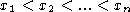 (very high time complexity)
(very high time complexity)
- the system of polynomial equations and its Grobner basis have
the same solution
- example
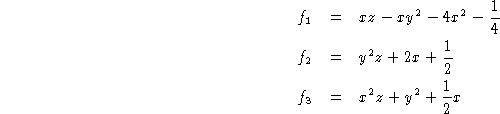
- Grobner basis of these polynomials with variables ordering
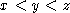
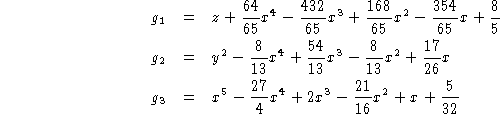
- this is in "triangular" form
-
 can be determined by solving the 3rd equation;
after substituting
can be determined by solving the 3rd equation;
after substituting 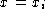 into the 2nd equation, we
can determine
into the 2nd equation, we
can determine 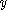 , etc.
, etc.
- one approximate solution is
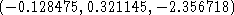
- solving (even numerically) of a polynomial equation in one variable
is much simpler than solving a system of polynomial equations
- solving a polynomial system is transformed into the successive
solution of equations in one variable; see the example
Grobner bases
Richard Liska