GCD of polynomials with integer coefficients

 

• now we consider polynomials from in one variable with integer coefficients

• pseudo-division of polynomials for which is defined by

  
  
  

  where and is the leading coefficient of the polynomial , i.e., the coefficient of the -th power of , so that the pseudo-quotient and the pseudo-remainder are also from

• then

• the polynomial is primitive if all its coefficients are mutually co-prime

  
  
  

• is the greatest common divisor of all coefficients of the polynomial and is the primitive part of the polynomial , hence,

• Euclidean algorithm for polynomial reminder sequence

    gcd := GCDPRS(a(x), b(x)) :=
          [suppose that degree of polynomial a is greater or equal to the
           degree of polynomial b, i.e., deg(a) >= deg(b)
           algorithms used:
             prem(a, b) - pseudo-remainder of polynomial a with polynomial b
             pp(a)      - primitive part of the polynomial a
             gcdi(j, k) - gcd of two integers j, k]
        1. A := pp(a)
           B := pp(b)
        2. while  B != 0  do
              r := prem(A, B)
              A := B
              B := r
           od
        3. return gcdi(cont(a), cont(b)) pp(a)

• coefficients and partial results grow very quickly--this algorithm is also not efficient

• it is possible to calculate the primitive part of the remainder in each step, however, the calculation of the primitive part requires the calculation of many greatest common divisors of integer coefficients which can often be large

• modular approach: perform calculations modulo a prime

  • apply homomorphism to coefficients

  • calculate the greatest common divisor of the transformed polynomials modulo

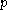
  • use the Chinese remainder algorithm for reconstructing the coefficients of the greatest common divisor back in the integers

 
• Example of GCD in Z[x]