Gradient je směr největšího poklesu, proto pokud
můžeme počítat parciální derivace, minimalizací ve
směru gradientu ušetříme ![]() kroků. Najdeme-li
v daném směru minimum, je další gradient kolmý k původnímu.
kroků. Najdeme-li
v daném směru minimum, je další gradient kolmý k původnímu.
Metoda největšího spádu může mít tedy podobný nedostatek jako
metoda pevných směrů ![]() velké množství malých kroků
pro úzká dlouhá údolí.
velké množství malých kroků
pro úzká dlouhá údolí. ![]() potřeba lepší volby směrů -
konjugované gradienty
potřeba lepší volby směrů -
konjugované gradienty
Pozn. Metoda využívá 1. parciálních derivací funkce ![]() ,
nepoužívá ale 2. parciální derivace.
,
nepoužívá ale 2. parciální derivace.
Funkci vyjádříme ve tvaru
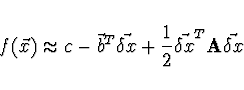
Nechť ![]() je
symetrická a pozitivně definitní v okolí minima.
Nechť
je
symetrická a pozitivně definitní v okolí minima.
Nechť ![]() ,
, ![]() jsou posloupnosti vektorů takové,
že
jsou posloupnosti vektorů takové,
že
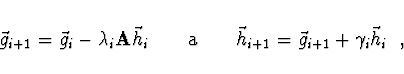
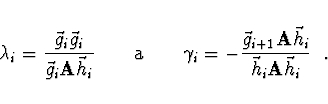
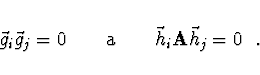 a
a
Pro kvadratickou formu lze ![]() a
a ![]() spočítat i bez
znalosti Hessovy matice A následovně
spočítat i bez
znalosti Hessovy matice A následovně
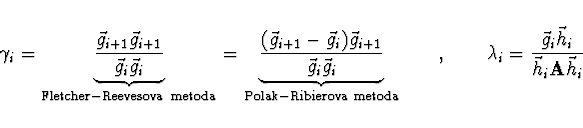
Při hledání minima budou vektory
![]() označovat směr největšího spádu a vektory
označovat směr největšího spádu a vektory ![]() směry hledání
minima ve směru - bodu
směry hledání
minima ve směru - bodu ![]() .
.
Postup hledání minima metodou konjugovaných gradientů:
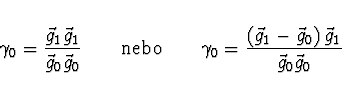
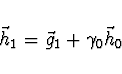
Pozn. Z metod, které využívají gradient a nepočítají 2. parciální
derivace, se často používají metody "proměnné metriky"
(BFGS - Broyden-Fletcher-Goldfarb-Shanno nebo
DFP - Davidon-Fletcher-Powell). Tyto metody jsou založeny
na postupné aproximaci inverzní Hessovy matice.