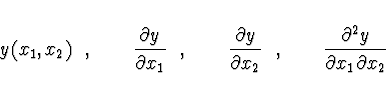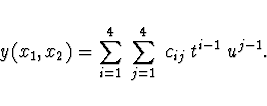

Next: Bikubický spline
Up: Interpolace ve 2 (více)
Previous: Globální interpolace
Jde o lokální interpolace Hermiteova typu. V každém bodě
![$(x_1[j], x_2[k])$](img204.gif) jsou zadány hodnoty funkce a jejích parciálních derivací
jsou zadány hodnoty funkce a jejích parciálních derivací
Jde tedy o 4 podmínky v každém ze 4 uzlů 2-rozměrného intervalu.
a tak lze určit 16 neznámých koeficientů 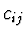 bikubické interpolace
bikubické interpolace
Jiri Limpouch
2000-03-24
![]() jsou zadány hodnoty funkce a jejích parciálních derivací
jsou zadány hodnoty funkce a jejích parciálních derivací