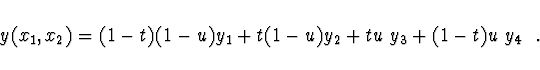

Next: Globální interpolace
Up: Interpolace ve 2 (více)
Previous: Interpolace ve 2 (více)
Interval ve dvou proměnných 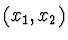 je znázorněn
na obrázku
je znázorněn
na obrázku
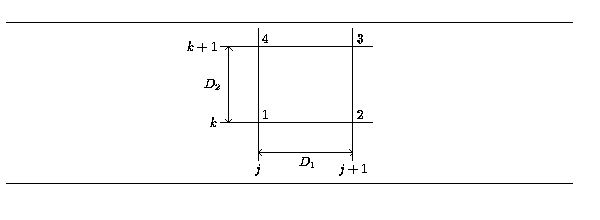
Hodnoty v jednotlivých bodech (viz obr. 1)
jsou zadány takto
![$y_1
\equiv y[j,k]$](img190.gif) ,
,
![$y_2 \equiv y[j+1, k]$](img191.gif) ,
,
![$y_3 \equiv y[j+1, k+1]$](img192.gif) a
a
![$y_4 \equiv y[j, k+1]$](img193.gif) .
.
Definujeme 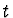 a
a 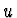 vztahy
vztahy
Pak má lokální interpolace tvar
Tato interpolace s bází
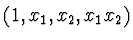 je lineární
v každé z proměnných
je lineární
v každé z proměnných 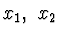 . Spojitost na hranicích intervalu
je zajištěna - na hranicích přímka, derivace ve směru kolmém k
hranici ovšem nemusí existovat.
. Spojitost na hranicích intervalu
je zajištěna - na hranicích přímka, derivace ve směru kolmém k
hranici ovšem nemusí existovat.
Jiri Limpouch
2000-03-24
![]() je znázorněn
na obrázku
je znázorněn
na obrázku

![]() ,
,
![]() ,
,
![]() a
a
![]() .
.
![]() a
a ![]() vztahy
vztahy
![\begin{displaymath}
t = \frac{x_1 - x_1[j]}{D_1}
\ \ , \quad \quad u = \frac{x_2 - x_2[k]}{D_2} \ \ .
\end{displaymath}](img196.gif)