

Next: Interpolace a extrapolace
Up: Aproximace funkcí
Previous: Aproximace funkcí
Aproximace funkce - výpočet funkčních hodnot
nejbližší (v nějakém smyslu) funkce v určité třídě funkcí
(funkce s nějakými neznámými parametry)
Příklady funkcí používaných pro aproximaci
- Polynom
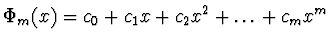 .
.
- Zobecněný polynom
kde
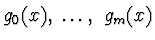 je systém m+1 lineárně nezávislých
jednoduchých a dostatečně hladkých funkcí.
je systém m+1 lineárně nezávislých
jednoduchých a dostatečně hladkých funkcí.
- Racionální lomená funkce
- Jiné.
Důvody aproximace - různorodé
- Příliš náročný výpočet funkce (složitý funkční předpis, implicitně
zadané funkce, ...)
- Potřeba výpočtu dalších charakteristik funkce
(derivace, integrál, ...)
- Analytické vyjádření není známo - funkce daná tabulkou hodnot
(spočtených či naměřených)
Typy aproximací
- Interpolační aproximace (interpolace a extrapolace) - hledáme takovou
funkci
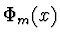 , která má v zadaných bodech
, která má v zadaných bodech
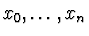 stejné
hodnoty (případně i derivace nejnižších řádů) jako funkce
stejné
hodnoty (případně i derivace nejnižších řádů) jako funkce 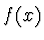 (prochází body zadanými v tabulce)
(prochází body zadanými v tabulce)
- Globální interpolace - v celém intervalu jsou koeficienty
interpolační funkce stejné (např. Lagrangeův či Newtonův interpolační
polynom, Hermiteova interpolace)
- Lokální interpolace - celý interval rozdělen na podintervaly a
v každém podintervalu má interpolační funkce jiné koeficienty
(např.
spline)
- Čebyševovy aproximace - hledáme
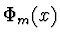 tak, aby se na zadaném
intervalu
tak, aby se na zadaném
intervalu
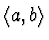 minimalizoval maximální rozdíl mezi
minimalizoval maximální rozdíl mezi 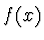 a
a 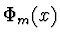 , tj. minimalizujeme
, tj. minimalizujeme
Nazývá se též nejlepší stejnoměrná aproximace. Používá se
často pro výpočet hodnot funkcí. K takové interpolaci lze dospět,
pokud zvolíme optimální hodnoty
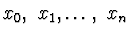 , ve kterých
funkci tabelujeme.
, ve kterých
funkci tabelujeme.
- Aproximace metodou nejmenších čtverců - minimalizujeme
Jde o spojitý nebo diskrétní případ aproximace metodou nejmenších čtverců.
U diskrétního případu je vždy 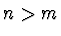 a tak funkce
a tak funkce 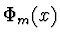 neprochází
neprochází
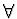 zadanými body.
Často se volí
zadanými body.
Často se volí 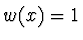 , pokud
, pokud
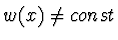 , pak mluvíme o vážené metodě
nejmenších čtverců a funkci
, pak mluvíme o vážené metodě
nejmenších čtverců a funkci 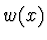 nazýváme vahou.
nazýváme vahou.
Pozn. Pokud cílem aproximace výsledků měření
metodou nejmenších čtverců není
jen nalézt přibližné funkční hodnoty, ale jde především o určení
hodnot koeficientů koeficientů
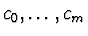 , stanovení přesnosti
určení těchto koeficientů a stanovení, zda je možno dobře aproximovat
naměřené hodnoty v dané třídě funkcí, úlohu nazýváme regrese
(vyrovnávací počet, modelování dat) a úloha patří do
statistického zpracování dat.
, stanovení přesnosti
určení těchto koeficientů a stanovení, zda je možno dobře aproximovat
naměřené hodnoty v dané třídě funkcí, úlohu nazýváme regrese
(vyrovnávací počet, modelování dat) a úloha patří do
statistického zpracování dat.


Next: Interpolace a extrapolace
Up: Aproximace funkcí
Previous: Aproximace funkcí
Jiri Limpouch
2000-03-24
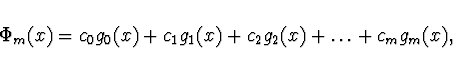
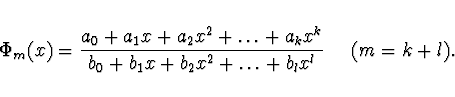
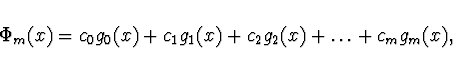
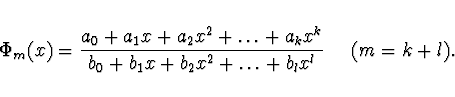
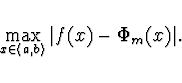
![\begin{displaymath}\hspace*{-4ex}
\int_a^b w(x)\ \left[ f(x) - \Phi_m(x) \right]...
... \ \sum_{i=0}^n w(x_i)\
\left[ f(x_i) - \Phi_m(x_i) \right]^2.
\end{displaymath}](img11.gif)